Algorithm
LeetCode算法题
17. 电话号码的字母组合 78. 子集 131. 分割回文串
Java 程序实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution_LC17 {
String[] alpha = new String[] {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
List<String> ans = new ArrayList<>();
char[] path = null;
String digits = null;
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) return new ArrayList<>();
this.digits = digits;
path = new char[digits.length()];
dfs(0);
return ans;
}
void dfs(int i) {
if (i == digits.length()) {
ans.add(new String(path));
return;
}
int d = digits.charAt(i) - '0';
for (char c : alpha[d].toCharArray()) {
path[i] = c;
dfs(i + 1);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution_LC78 {
List<List<Integer>> ans = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int[] nums = null;
public List<List<Integer>> subsets(int[] nums) {
this.nums = nums;
//dfs(0);
_dfs(0);
return ans;
}
// input-view
void dfs(int i) {
// 1.terminator
if (i == nums.length) {
ans.add(new ArrayList<>(path));
return;
}
// 2.drill down
dfs(i + 1); // not select
path.add(nums[i]); // select
dfs(i + 1);
path.remove(path.size() - 1); // recover
}
// answer-view
void _dfs(int i) {
ans.add(path);
for (int j = i; j < nums.length; j++) {
path.add(nums[j]);
dfs(j + 1);
path.remove(path.size() - 1);
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution_LC131 {
List<List<String>> ans = new ArrayList<>();
List<String> path = new ArrayList<>();
String s = null;
public List<List<String>> partition(String s) {
this.s = s;
//dfs(0);
_dfs(0, 0);
return ans;
}
// answer-view
void dfs(int i) {
// terminator
if (i == s.length()) {
ans.add(new ArrayList<>(path));
return;
}
// drill down
for (int j = i; j < s.length(); j++) {
if (isPalindrome(i, j)) {
path.add(s.substring(i, j + 1));
dfs(j + 1);
path.remove(path.size() - 1);
}
}
}
// input-view
void _dfs(int i, int start) {
if (i == s.length()) {
ans.add(new ArrayList<>(path));
return;
}
if (i < s.length() - 1) {
_dfs(i + 1, start);
}
if (isPalindrome(start, i)) {
path.add(s.substring(start, i + 1));
// why second param is i+1 not start+1?
_dfs(i + 1, i + 1);
path.remove(path.size() - 1);
}
}
boolean isPalindrome(int left, int right) {
while (left < right) {
if (s.charAt(left++) != s.charAt(right--)) {
return false;
}
}
return true;
}
}
Review
- 只是一个脑图,印象不很深刻
- 损失精度换取速度
- 搜索快、插入快,不支持删除
- 经典使用场景:1 判断URL是否高危需要额外检查(chrome), 2 判断密码太弱提示用户更改
- B[h1(x)] = ::: = B[hk(x)] = 1, K个哈希函数
- 发现其中BUG(Example 4.1), 给作者发了Email
Tip
缓存穿透
{不存在的Key, 请求打到数据库}

-
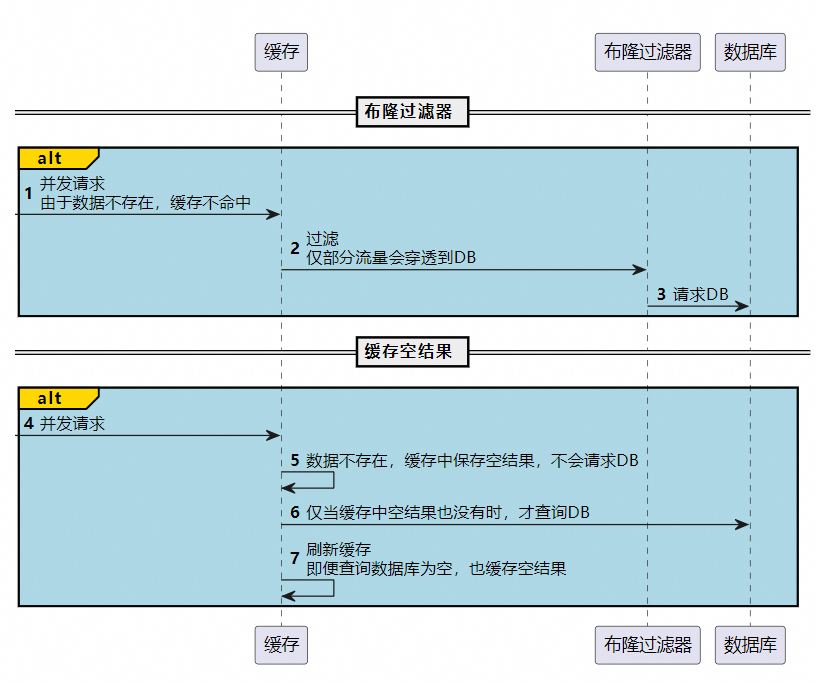
定义 缓存穿透是指查询一个数据库中不存在的数据,由于缓存不命中(因为数据根本就不存在),请求便会穿过缓存,直接请求数据库。如果有大量此类请求,数据库压力会突然增大,严重时可能会拖垮数据库。
-
应对策略
- 1)布隆过滤器:在缓存之前使用布隆过滤器,一种空间效率高的数据结构,用来检测一个元素是否在一个集合中。如果布隆过滤器说不存在,那么就直接返回,不再查询数据库。
- 2)缓存空结果:如果查不到数据,也将这个“空”结果缓存起来,并设置一个合理的过期时间。
缓存击穿
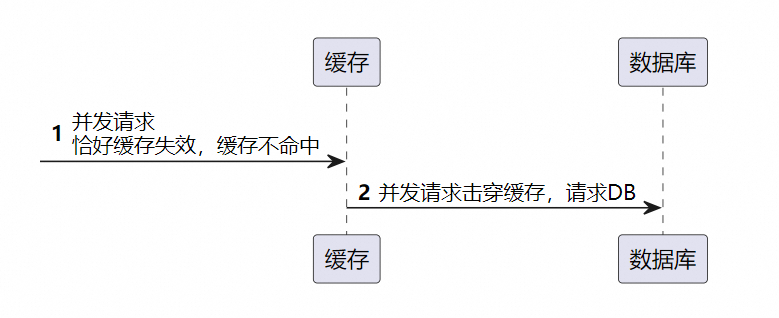
{A Hot Key失效, 请求打到数据库}
-
定义 缓存击穿指一个热点 key 在缓存中有效期过期的瞬间,大量请求同时涌入数据库去查询这个数据,因为缓存过期这些请求不能被缓存拦截,直接请求到数据库,导致数据库瞬间压力过大。
-
应对策略
- 1)设置热点数据永远不过期:这要求系统能准确判断哪些是热点数据。
- 2)加锁或队列:当热点 key 过期时,不是所有请求都去数据库查询,而是让某一个请求去数据库查询并更新缓存,其他请求等待缓存更新后再访问缓存。
缓存雪崩
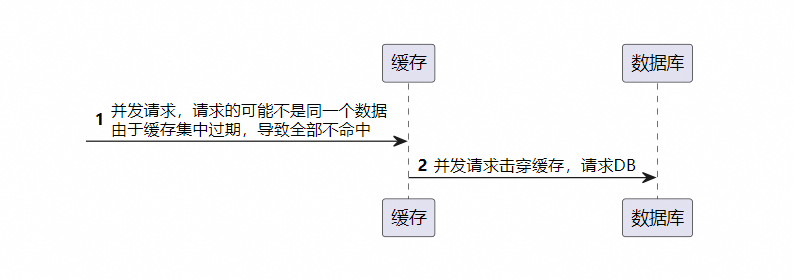
{大量的Key同时失效, 请求打到数据库}
-
定义 缓存雪崩是指在某一个时间段内,大量的缓存键集中过期失效,导致所有的请求都落到数据库上,造成数据库瞬间压力过大可能到达崩溃的状态。
-
应对策略
- 1)缓存数据的过期时间设置为随机,防止很多缓存同时过期。
- 2)使用高可用的缓存架构,即使缓存服务出现问题,也能通过备份机制快速恢复。
- 3)设置热点数据静态化,即把访问量较大的数据做静态化处理,减少数据库的访问。
数据一致性问题
-
case 数据一致性问题是指当数据在多个地方(如缓存和数据库)存储时,这些地方的数据可能会出现不一致的情况。这种不一致可能是由于缓存更新滞后、系统故障或其他原因引起的。数据一致性是分布式系统设计中的一项挑战,尤其是在读写非常频繁的系统中。当数据被更新时,如果缓存中的相应数据没有立即更新,那么缓存系统将向应用程序提供旧数据。这会导致应用程序得到不一致的结果,影响用户体验和数据的准确性。
-
solution 在分布式系统中,数据一致性是一个核心问题。根据系统的设计与需求,可以选择实时强一致性(Strong Consistency)或最终一致性(Eventual Consistency)。
实时强一致性 CP
-
定义 实时强一致性保证了任何时刻,所有的客户端看到的数据都是一样的。在分布式系统中实现强一致性意味着,一个操作一旦完成,所有的客户端立即都能看到这个操作的结果。
-
适用场景 事务性强、对数据一致性要求高的系统,如银行系统或任何财务系统。
-
保障策略 1)三阶段提交(3PC)等分布式事务协议:在分布式系统中保证操作要么全部成功,要么全部失败。 2)分布式锁:通过在操作前获取全局锁,保证同一时刻只有一个操作可以修改数据,从而保障数据一致性 3)强一致性算法:如 Paxos 或 Raft 算法,通过一系列严格的消息传递和确认机制,确保分布式系统中的多个副本能够达到一致状态。
最终一致性 AP
-
定义 最终一致性是指系统会保证在没有新的更新操作的情况下,经过足够的时间后,数据将达到一致的状态。在这种模型下,数据的副本之间可能会暂时存在不一致。
-
适用场景 对实时性要求不高,可以容忍短时间内数据不一致的场景,如社交网络、推荐系统等。
-
保障策略 1)异步复制:当数据更新发生时,首先更新主副本,然后异步地将更新同步到其他副本。 2)读取修复(Read Repair):在读取数据的时候检测副本之间的不一致,并在后台异步修复不一致的数据。 3)后台一致性修复进程:定期在后台运行的进程检查和同步数据副本之间的差异,以达到最终一致性。 4)版本控制:每次更新数据时附加一个时间戳或版本号,用于解决更新冲突和保持数据的最终一致性。
常见缓存更新/失效策略
缓存更新策略
-
Write through cache(直写缓存):首先将数据写入缓存,然后立即将新的缓存数据复制到数据库。这种方式可以保证写操作的一致性,但可能会影响写操作的性能。
-
Write back cache(写回缓存):数据首先写入缓存,然后由缓存异步写入数据库。这种方式可以提高写操作的性能,但增加了数据丢失的风险。
-
Write around cache(绕写缓存):绕过缓存,直接写数据库,然后依据需要更新缓存或使缓存失效。这适用于更频繁读取操作的场景。
缓存失效策略
- 主动更新:当数据库数据变化时,主动更新缓存中的数据。这可以保持缓存数据的实时性,但可能会增加系统的复杂性。
- 定时失效:为缓存数据设置一个过期时间。定期从数据库中重新加载数据,以保持数据的新鲜度。但这无法解决数据在两次加载之间变化导致的一致性问题。
- 惰性加载:只有在请求特定数据且发现缓存失效或缓存中没有该数据时,才去数据库加载该数据。这种策略简单,但在高并发场景下可能会导致缓存击穿。
数据一致性解决方案
使用缓存一致性协议
- 基于订阅的更新:使用消息队列(如Kafka,RabbitMQ)来发布数据库更新,然后相关服务订阅这些更新消息来同步更新缓存。
- 最终一致性:采用最终一致性模型,允许系统在一段时间内是不一致的,但保证经过足够的时间后,系统中的所有复制数据最终将达到一致的状态。
分布式缓存系统
- 使用如Redis Cluster、Apache Ignite、Tair等分布式缓存系统,这些系统内置了处理缓存一致性的机制,(但是无法解决缓存和数据库之间的数据一致性问题)。
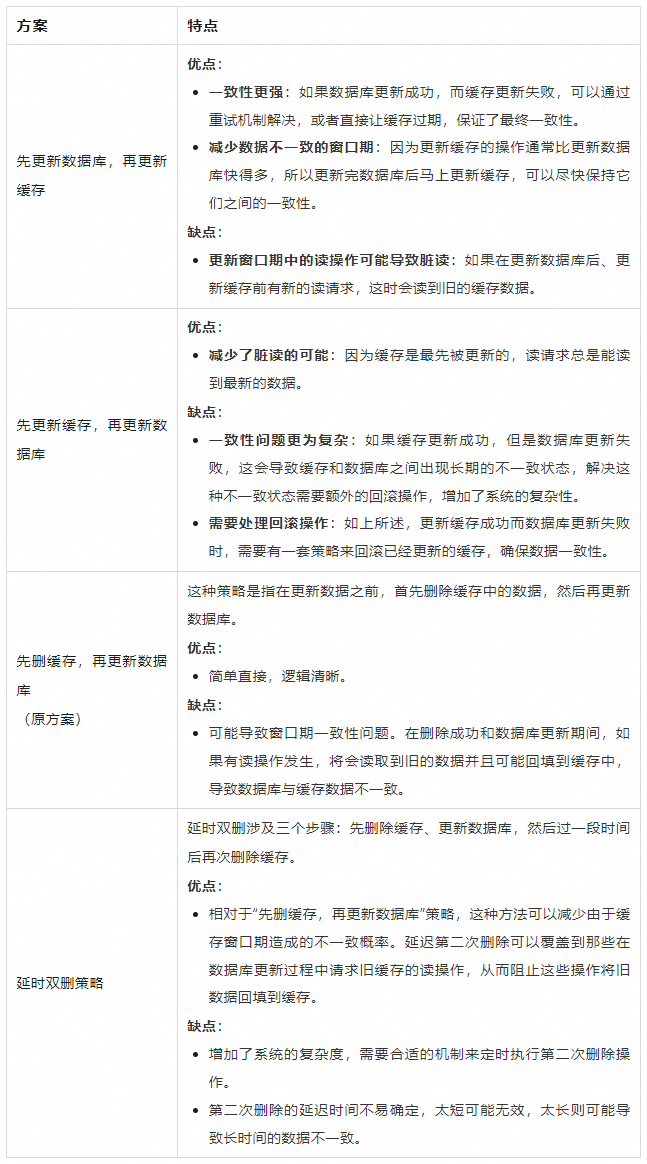
各方案及优缺点
- 先更新缓存
- 先更新数据库
- 先删缓存
- 延迟双删
曾经落地方案(某信Med)
- 本地缓存带有失效时间
- 本地缓存标准情况下不缓存空值
- 数据库更新完成,事务未提交时,在事务内发布删除缓存消息
Share
回溯算法
回溯算法是一种通过穷举来解决问题的方法,其核心思想是从一个初始状态出发,暴力搜索所有可能的解决方案。当遇到正确的解时,将其记录,直到找到解或尝试了所有可能的选择都无法找到解为止。回溯算法通常采用“深度优先搜索”来遍历解空间,适用于组合问题、排列问题、子集问题等。在实际应用中,回溯算法通过逐步构建问题的解,并在发现当前解不可行时返回上一状态进行调整,直到找到一个满足要求的解。
解题思路
- 1.从多重循环到回溯 LC17.电话号码的字母组合
- 2.回溯三问: 思考回溯问题的套路 {一:当前操作or每一步操作? 二:子问题? 三:下一个子问题?}
- 3.子集型回溯 LC78.子集 LC131.分割回文串 -> {①子集型回溯, ②组合型回溯, ③排列型回溯}
- 4.两种思路 输入的视角 答案的视角
子集型回溯习题集
- LC17
- LC78
- LC131
组合型回溯习题集
- LC77
- LC216
- LC22
排列型回溯习题集
- LC46
- LC51
个人心得
- 子集型 组合型 : 1) 不选或者选[no select / select, 输入视角 input-view] 2) 枚举选哪个[1->K, 答案视角 answer-view], 组合型可以通过约束条件剪枝[pruning]
- 排列型 : 每一步操作都需要选择,只有[select]
- 树形结构 {dfs:遍历} {bfs:最短路径}
- 一个视角是指[树]的视角,两种思维模式是指[遍历:全排列:递归函数没有返回值,通过全局变量]和[分解问题:斐波那契数列:递归函数有返回值,向上传递]两种思维模式。
- 与动态规划的联系